1. Introduction¶
Welcome to discrete mathematics: the mathematics of discrete as opposed to smoothly varying quantities.
A good example of a smoothly varying set of quantities is the real numbers. The real numbers vary smoothly in the sense that there are no gaps between them. Between any two real numbers there is another, and if an infinite sequence of such numbers gets ever closer to some limit, that limit is a real number, too.
Everyday algebra and calculus involve functions that take real numbers as arguments and that return real numbers as results. Discrete mathematics, by contrast, concerns quantities separated from adjacent quantities
One familiar example of a set of discrete values is the set of the natural numbers: the whole numbers from zero on up. There is no natural number between any two adjacent natural numbers. The natural numbers are thus discrete. The field of mathematics called number theory concerns the integers, especially prime numbers. Other examples include the truth values of Boolean algebra; finite and certain infinite sets; lists; relations; graphs; finite automata; and the propositions and proofs of various logics. Don’t worry if you aren’t yet familiar with all of these terms.
These topics, and other topics in discrete mathematics, are essential to both the theory and practice of computer science. Major topics to be covered in this course include logic, set theory, finite automata, inductive definitions, formal languages, and aspects of computational complexity.
The overall aim of this course is to prepare you to use formal (mathematically precise) reasoning in your future studies and work in computer science. Areas of computer science in which such reasoning is essential include algorithms and data structures, the theory of computing, cryptography, computer security and privacy, and software engineering.
To achieve this central aim will require advances in several areas of intellectual development. They include increased mathematical maturity, or the ability to think much more abstractly about mathematical objects and operations; the development of fluency in the languages of mathematical logic and proof construction; understanding how logic and computation are deeply connected; learning to use modern tools for the automation of logic and logical reasoning; and seeing how all of these ideas play out in various aspects of computer science.
1.1. Mathematical Maturity¶
Discrete mathematics is also the field in which you will make two major transitions in your understanding of mathematics. The first is from understanding mathematics as a field about numbers to understanding it as being about precisely defined quantities of any kind.
Consider two examples. The Boolean truth values, 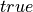 and
and 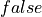 , are not numbers, but there is nevertheless a rich and vitally important algebra involving these non-numerical objects. For example, the expression,
, are not numbers, but there is nevertheless a rich and vitally important algebra involving these non-numerical objects. For example, the expression, 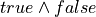 evaluates to
evaluates to 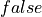 . Similarly, there is an algebra of character strings, or finite lists of non-numerical characters. If
. Similarly, there is an algebra of character strings, or finite lists of non-numerical characters. If 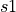 and
and 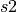 name any two strings (e.g., “Hello, ” and “World”), then we can define the expression,
name any two strings (e.g., “Hello, ” and “World”), then we can define the expression, 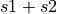 , to mean the string obtained by appending
, to mean the string obtained by appending 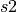 to
to 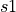 (e.g., “Hello, World!”). Mathematical reasoning thus also applies to non-numerical objects and operations.
(e.g., “Hello, World!”). Mathematical reasoning thus also applies to non-numerical objects and operations.
The second transition you will make in this class is from understanding mathematics as being concerned with computing solutions, to viewing it as a field concerned with expressing mathematical propositions, or claims that certain states of affairs prevail in certain worlds, and proving that such propositions are true. Mathematics is as much about what is mathematically true as it is about solving problems.
Consider a remarkable example. Mathematicians struggled for over three centuries to determine whether or not it is true that there are three distinct, positive integers  ,
, 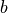 , and
, and  , that satisfy the equation
, that satisfy the equation 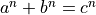 for some integer,
for some integer, 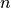 , greater than
, greater than 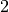 . The proposition that there is no such combination of values is known as Fermat’s Last Theorem. People had looked at many 4-tuples of numbers and had never found one that satisfies the equation. But it remained unclear whether there might be a combination of four integers out there that would satisfy the equation. It wasn’t until 1994 that Andrew Wiles finally proved (albeit informally) that Fermat’s Last Theorem is true. We now know for sure (or almost for sure, as there is no formalized and mechanically checked proof) that no one will ever find three disctinct, positive integers,
. The proposition that there is no such combination of values is known as Fermat’s Last Theorem. People had looked at many 4-tuples of numbers and had never found one that satisfies the equation. But it remained unclear whether there might be a combination of four integers out there that would satisfy the equation. It wasn’t until 1994 that Andrew Wiles finally proved (albeit informally) that Fermat’s Last Theorem is true. We now know for sure (or almost for sure, as there is no formalized and mechanically checked proof) that no one will ever find three disctinct, positive integers,  ,
, 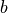 ,
,  , and an
, and an 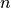 , where
, where  , such that
, such that 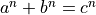 .
.
1.2. Logical Reasoning¶
A proposition is a claim that some state of affairs holds in some domain of discourse. In the preceding example, the domain of discourse is that of the integers. And the state of affairs that was claimed to hold was that there are no such four integers that satisfy the equation. We now know that it is true that such a state of affairs holds in the domain of the integers.
To establish the truth of such a proposition in mathematics, one must exhibit what mathematicians, logicians, and computer scientists call a proof. A proof shows that such a conclusion follows by the application of valid logical reasoning steps from the unquestioned, foundational axioms of a given mathematical system.
In a consistent logic, from premises that are true, and by the correct application of valid inference rules, one can only deduce conclusions that are also true. That is a picture of what we can view as forward reasoning: from axioms to conclusions. When asked to prove that some proposition, a conclusion, is true, what one must show is that it can be deduced from axioms. If one looks at it the other way around, what is needed is to show that its can be deduced from the truth of simpler propositions, and that this backwards chain can be traced all the way back to axioms. Such “chains” of applications of reasoning rules, ultimately grounded in axioms, are called proofs.
As an informal example, consider the proposition, there is no largest natural number. Intuition suggest that this proposition is true. But to establish beyond any doubt that there is no largest natural number, or to establish the truth of any mathematical conjecture, we have to exhibit a proof that it is true.
So how can we prove there is no largest natural number? Here is a rigorous but informal (natural language) proof. By informal we mean that the proof is not itself formulated as a mathematical object but rather is given as an argument in natural language, here in English.
To prove that there is no largest natural number we will start by assuming that there is one, and we will then show that this assumption leads to a contradiction. In a consistent logic, which ours is, the only way to deduce a false conclusion is to start with a false premise, or assumption. So if the assumption that there is a largest natural number leads by valid logical reasoning to a contradiction (a falsity) the the assumption itself must have been fase. We will thus obtain a proof that it is false that there’s a largest natural number.
Here’s the proof. Assume there is a largest natural number. If there exists such a number, we can give it a name. Let’s call it 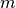 . Our assumption implies that there is a proof that
. Our assumption implies that there is a proof that 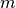 is the largest natural number. Now consider the natural number,
is the largest natural number. Now consider the natural number, 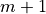 . Using the axioms of natural number arithmetic, we can prove (though we don’t do this explicitly here) that this value is larger than
. Using the axioms of natural number arithmetic, we can prove (though we don’t do this explicitly here) that this value is larger than 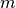 . Now we have two proofs: one, a proof that
. Now we have two proofs: one, a proof that 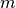 is the largest natural number; the other, a proof that there is no largest natural number. Our assumption led to a contradiction, so it must have been false. This proves that there is no largest number.
is the largest natural number; the other, a proof that there is no largest natural number. Our assumption led to a contradiction, so it must have been false. This proves that there is no largest number.
1.3. Role in Computer Science¶
Proofs are essential in computer science. For example, to establish the truth of a proposition that software meant to secure online financial transactions really is secure requires not just the intuition of the programmer, which is generally faulty, but a proof that the program is secure. The concept of mathematical proofs extends to objects that include computer programs!
Computer scientists use proofs to establish truths of important propositions in many areas of computer science. Proofs are used to show that new algorithms have desirable efficiency properties. They are used to show that certain kinds of problems have no efficient algorithmic solutions, or to prove that they have no algorithmic solutions at all. For example, it has been proved that no algorithm can decide with absolute precision whether any given computer program will go into an infinite loop of not.
Proofs are used to show that encryption schemes are hard to break. They are used to show that given programs correctly implement specifications written in mathematical logic. They can be used to show that the file systems that store data in computers will not be corrupted, resulting in loss of data, when computers crash at random times, e.g., due to electrical outages. They are used to prove that the device drivers that operating systems use to interact with hardware devices can’t corrupt operating system data structures leading to computer crashes. They are produced automatically by compilers for such languages as Java and C++ that it is not possible for a programmer to mistakenly apply an operaton to a data item of a type to which it should not be applied.
The concept of logical proofs is at the heart of computer science. Indeed the field of compter science itself evolved out of work in the 1930s and 1940s, by the likes of Gödel, Turing, and Church, that sought to prove propositions about what is and is not provable in mathematical systems in general.
In this class, you will therefore learn about mathematical logics, which are languages in which propositions can be made mathematically precise; about logical inference rules, which are rules for deducing the truths of new propositions from truths already established or assumed; and about proofs, which are mathematical objects that establish the truths of given propositions by showing that there are chains of such inferences connecting directly or indirectly all the way back to the axioms, or unquestioned truths, of given mathematical systems.
1.4. Automated Reasoning¶
Both the proposition above (that there is no largest natural number) and the proof we gave are informal. In this case, the claim and its proof are simple enough that there is not much question we got them right. Yet the history of mathematics and of computer science is replete with informal proofs that later on were found to be flawed.
Today, computational tools are emerging that treat both propositions and proofs as formal, mathematical, and indeed computational, objects. We will use such a tool in teaching this class. This approach will help you learn to write and reason about logical propositions and proofs as carefully as you write computer programs. You will have at your disposal a tool that will help you understand, apply, and verify the correct application of all the basic rules of mathematical logic, as well as any new rules that might create.
1.5. Course Content and Organization¶
By the end of this class you will have developed initial mastery of the higher-order constructive logic that such tools use, of the predicate logic of everyday mathematics, and of a diversity of topics in discrete mathematics that are themselves deeply rooted in these logics. These topics include natural deduction proof theory, set theory, relational algebra, the theory of finite automata, inductive definitions of various types including the natural numbers, recursive functions, the syntax and semantics of formal languages and of propositional logic in particular, and the theory of Boolean satisfiability.
The remainder of this course is divided into several major sections. The first section, comprising a significant part of this course, provides the logical foundations for the rest of the course. The second section covers set theory, showing in particular how it rests on these logical foundations. The third section delves further into set theory with a focus on the relations on a set. The fourth section explores a crucial computer science applications of relational algebra, in the theory of finite automata. Section five introduces inductive definitions, which provide for the introduction of new types of mathematical and computational objects into consideration, including Boolean values, natural numbers, lists, along with the often recursive definition of functions involving such objects and techniques of proof by induction for propositions involving such objects. Section six builds on the preceding sections to show how the syntax and semantics of formal logic can itself be formalized. In section seven, we will formalize the syntax and operational semantics of propositional logic, a simple logic of Boolean expressions. In section eight, we will explore the computational complexity of deciding whether or not a given expression in propositional logic is true.